Type inference in ogma using graphs

ogma is a scripting language focused on processing tabular data, written in Rust. Follow the development of type inference along this branch.

Type inference in ogma is the ability to induct the types of all inputs, outputs, and arguments without needing prompting from the user. It does this by propagating known types amongst implementations. It makes writing expressions such as filter col --Str = 'foo' more simple by allowing the elision of the type flag: filter col = 'foo'.

ogma's compilation system is currently sequential, processing one block at a time, in order. This makes the type propagation in the forward direction extremely robust, a block can only be compiled when a known input type is supplied. Implementing type inference breaks this implementation. For example, the expression filter col = 'foo' must allow for flexibility of the input feeding into the expression = 'foo'. To solve this issue, the compilation system needs to be refactored such that partial compilation is supported. The use of a graph data structure is prototyped as a means of allowing partial compilation, type propagation in both forwards and backwards directions, and general type inferencing.

The graph structure library being developed with is petgraph. This library implements graphs by index rather than reference, which is useful for maintaining multiple graphs indexing the same nodes. Each node carries a weight of data (type W), and each edge also carries a weight of type E.

Flattening the AST

To achieve the type propagation, the relationship of each node in the AST needs to be understood. The current AST is a typical tree structure with a recursive enum definition. This structure does not allow for random access, which is needed for partial compilation, i.e. the ability to compile a block without carrying the ancestor hierarchy. The solution? Represent the AST in a graph! The graph is mostly a simple tree structure, with forking at the expressions (to multiple 'child' blocks) and at blocks (to multiple 'child' terms).

Since the graph is reproducing the AST, each node's weight represents an AST node, and is represented with an enum of node variants. Similarly, the edges are represented with an enum. Usually an edge weight is Normal, however with an op node, information about the terms and, if specified, the input type is required. This information is carried with the Term(u8) (a positional index of the term) and they Keyed(Option<Type>) variants.

// NODE WEIGHT
pub enum AstNode {
    Op { op: Tag, blk: Tag },
    Intrinsic { op: Tag },
    Def(Vec<Parameter>),
    Flag(Tag),
    Ident(Tag),
    Num { val: Number, tag: Tag },
    Pound { ch: char, tag: Tag },
    Var(Tag),
    Expr(Tag),
}
// EDGE WEIGHT
pub enum Relation {
    Normal,
    Keyed(Option<Type>),
    Term(u8),
}

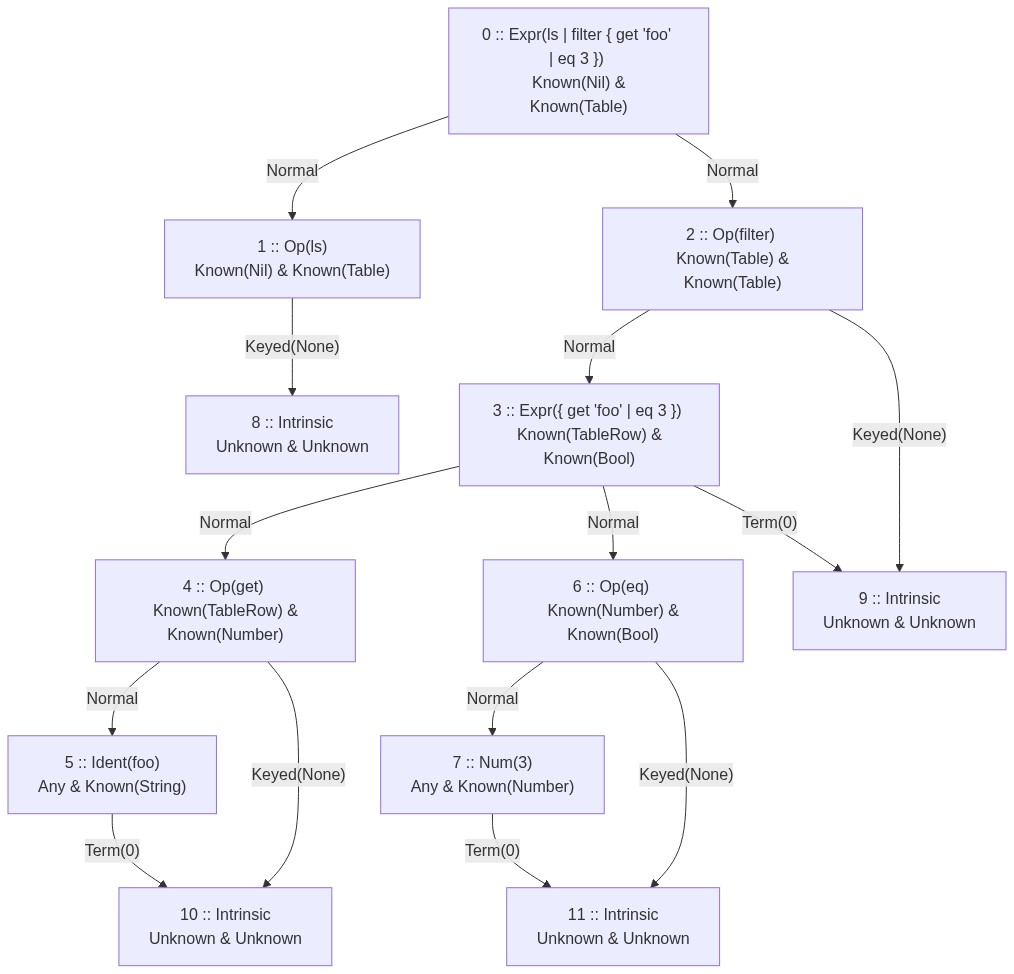
As an example, the expression ls | filter { get 'foo' | eq 3 } would flatten into the following flowchart. This chart has the types annotated after compilation was completed (more on that later). Notice how the forking of expressions goes to the _op_ node, which then links to the term(s). The _op_ node also has Keyed and Term edges, which, in this case, terminates into intrinsic implementations, but are used further in user defs.

Type graph

Type inferencing in ogma is complicated by the lack of strict definition signatures. For example, the filter op takes an expression which supplies a TableRow as input, but the output of the expression is derived from what the expression is made of. This makes definitions polymorphic, but not general. Using a graph to track type knowledge about the AST nodes allows for multiple methods of inference:

1. By deduction with transitive type flow,
2. By testing various input types for compilation, and
3. By feedback from partial compilation.

The type graph uses the same nodal structure as the AST graph. That is, a node index into the AST graph points to the same node in the type graph. For the type graph weights, each AST node can have knowledge about its input and output type. The edges in the type graph describe the flow of type information, along with how it flows (see the code below).

// Type graph node weight
pub struct Node {
    pub input: Knowledge,
    pub output: Knowledge,
}
pub enum Knowledge {
    Unknown,
    Any,
    Known(Type),
    Obliged(Type),
    Inferred(Type),
}
// Type graph edge weight
pub enum Flow {
    /// Output knowledge flows into the input.
    OI,
    /// Input knowledge flows into the input.
    II,
    /// Output knowledge flows into the output.
    OO,
    /// Input knowledge flows into the output.
    IO,
}

The structure of the AST graph drives much of the type graph structure, not by following the tree structure, but by making the following observations:

1. The input of an expression goes to the input of the first op,
2. The output of the last op in an expression goes to the output of the expression,
3. The output of a block goes to the input of the next block,
4. The input into an op which links to a definition would flow the input down into the expression (and back out again)

Using these connections a type graph can be constructed like below.

Not all nodes need to be connected! Nodes which are terms do not generally have a known flow to them. Instead, they can feed their type information or obligations back into the type graph as the compilation loop takes place.

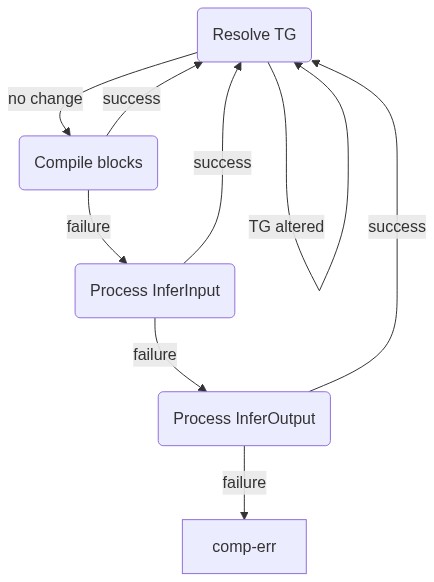
Compilation loop

The original compilation algorithm was linear. It would recursively resolve a block, and either the block would compile or it would return an error. To support partial compilation, a loop is required which can try a compilation, gain information about the types, and loop back to try compilation again, armed with the new information. The implementation details are glossed over, but the loop consists of resolving the type graph (flowing the available types along the edges), attempting to compile blocks which have known inputs, inferring input types into blocks by compilation attempts with various types, and inferring output types out of blocks (again by trial and error).

Each step is gated on whether new information is obtained, and eventually the type graph would resolve enough to allow a full compilation, or no new information would be obtained and the loop would exit with an error condition.

Variables

One obstacle to implementing partial compilation is the variable tracking. The current variable system is sequential. Bugs can be introduced if blocks are to be compiled (or attempted to compile) out of sequence, since the variable tracking system would not be considered 'up-to-date'. However, only a slight change is needed to gain partial information, an Option type! Currently, a Locals struct is passed between block compilations, which gets updated with let calls (and sometimes manually), and can be referenced when a variable shows up. This behaviour is required and only works on an up-to-date Locals, since variable shadowing is supported. If, however, a block does not interact with the Locals, it can still compile. So a slight change to have a reference to an Option<&mut Locals> allows for blocks to compile even if there is no Locals, but will fail compilation if there is no Locals, yet the block needs to interact with one.

While prototyping, it was found there is actually a soundness bug in nested manual variables. This was good to find and shows that this new system is likely to be more rigorous for variables. The bug has been lodged here: https://github.com/kdr-aus/ogma/issues/42

To handle reverting the locals on compilation failure, a clone of the locals is made beforehand, and reversion is simply not updating the original with the altered value!

Current state

The type-inference branch in the ogma repository is tracking the development of type inference. The compilation prototype using graphs as the main compilation data structure, as outline in this post, is done and looks promising. With the prototype completed, the implementations and tests need to be wired back together, and this will further test the robustness of the system and show any bugs. While the inferencing side has been prototyped, the next development feature is to add an annotation system, allowing a user to ergonomically annotate their types (since type inference is not omniscient!).